VECTOR

 

🌑 Vectors :

There are quantities in physics and science characterized by both magnitude and direction, such as displacement, velocity, force, and acceleration. To describe such quantities, we introduce the concept of a vector as a directed line segment  from one point P to another point Q. Here P is called the initial point or origin of  , and Q is called theterminal point, end, or terminus of the vector. We will denote vectors by bold-faced letters or letters with an arrow over them. Thus the vector PQ maybe denoted by A or 

as in Fig. 1 (a). The magnitude or length of the vector is then denoted by |PQ|, |A|, || or A.The following comments apply.

● Two vectors A and B are equal if they have the same magnitude and direction regardless of their initial point. Thus A = B in Fig. 1 (a).

● A vector having direction opposite to that of a given vector A but having the same magnitude is denoted by -A (see Fig. 1 (b)] and is called the negative of A.

🌑 Scalars :

   Other quantities in physics and science are characterized by magnitude only , such as mass , length , and  temperature. Such quantities are often called scalars to distinguish them from vector. However , it must be emphasized that apart from units , such as feet , degree , etc., Scalars are nothing more than real numbers. Thus we can denote them, as usual , by ordinary letters . Also , the real numbers 0 and 1 are part of our set of scalars.

■ Note:  

Unit vector:  

Unit vectors are vectors having unit length. Suppose A is any vector with length |A|>0. Then `(bb"A")/ (|bb"A"|)` is a unit vector , denoted by a , which has the same direction as A . Also , and vector A may be represented by a unit vector a in the direction of A multiplied by the magnitude of A . That is, A = |A|a.

EXAMPLE : Suppose  `|\hat{A}|` =3. Then `\hat{a} = |\hat{A}|/3` is a unit vector in the direction of A. Also, A= 3`\hat{a}` .

● Rectangular Unit Vectors `\hat{i}\,\hat{j}\,\hat{k}` : 

An important set of unit vectors, denoted by `\hat{i}\,\hat{j}\ and \hat{k}` are those having the directions, respectively, of the positive x, y, and z axis of a three-dimensional rectangular coordinate system. (Fig -2). 

The coordinate system shown in (Fig - 2 ) which we use unless otherwise stated, is called a right handed coordinate system. The system is characterized by the following property. If we curl the fingers of the right hand in the direction of a 90° rotation from the positive x-axis to the positive y-axis, then the thumb will point in the direction of the positive z-axis.

Generally speaking , suppose nonzero vectors A,B,C have the same intial point and are not coplanar. The A,B,C are said to form a right handed system or dextral system if a right threaded screw rotated through an angle less than 180° from A to B will advance in the direction C as shown in (fig -2)

■ Note 2 : 

Components of a vector : 

Any vector in three dimensions can be represented with an initial point at the origin O = (0, 0, 0) and its end point , say, ( , , ). Then the vectors `A_1\hat{i}, A_2\hat{j}, A_3\hat{k}` are called the component vectors of in the x, y, z directions, and the scalars A₁ , A₂ , A₃ are called the components of in the x, y, z directions, respectively.

The sum of ,  and  is the vector , so we may write

= `A_1\hat{i}+A_2\hat{j}+A_3\hat{k}`

The magnitude of follows:

|| = `\sqrt{A_1^2 + A_2^2 + A_3^2}`

Suppose =`A_1\hat{i}+A_2\hat{j}+A_3\hat{k}` and =`B_1\hat{i}+B_2\hat{j}+B_3\hat{k}` .Then 

   ■  +  = `(A_1+B_1)\hat{i}+(A_2+B_2)\hat{j}+(A_3+B_3)\hat{k}`

   ■ m = m(`A_1\hat{i}+A_2\hat{j}+A_3\hat{k}`) = `(mA_1)\hat{i}+(mA_2)\hat{j}+(mA_3)\hat{k}`

🌑 Vector addition :

     ● Law of Triangle of vectors:

Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.

To obtain  which is the resultant of the sum of vectors   and with the same order of magnitude and direction as shown in the figure, we use the following rule: = +  

        ● Derivation : 

           Consider two vectors  and  that are represented in the order of magnitude and direction by the sides OA and AB, respectively of the triangle OAB. Let be the resultant of vectors   and .

From triangle OCB, 

OB² = OC² + BC²

OB² = (OA+AC)² + BC² ...........(eq.1)

In triangle ACB with θ as the angle between and 

`\cos\theta = (AC)/(AB)`

AC = ABcosθ = Qcosθ

`\sin\theta = (BC)/(AB)`

BC = ABsinθ= Qsinθ

Substituting the values of AC and BC in (eq.1), we get

R² = (P + Qcosθ)²+(Qsinθ)²

R²= P²+ 2PQcosθ + Q²cos²θ + Q²sin²θ

R² = P² + 2PQcosθ + Q²

therefore, `R=\sqrt{(P^2+2PQcos\theta+Q^2)}`

Above equation is the magnitude of the resultant vector.

To determine the direction of the resultant vector, let Φ be the angle between the resultant vector R and P.

From triangle OBC,

tanΦ=`(BC)/(OC)=(BC)/(OA+AC)`

tanΦ = `(Qsin\theta)/(P+Qcos\theta)`

therefore, Φ=`tan^(−1)[(Qsin\theta) / (P+Qcos\theta)]`

Above equation in the direction of the resultant vector.

     ● Law of parallelogram of vectors :

Parallelogram law states that the sum of the squares of the length of the four sides of a parallelogram is equal to the sum of the squares of the length of the two diagonals. In Euclidean geometry, it is necessary that the parallelogram should have equal opposite sides.

If ABCD is a parallelogram, then AB = DC and AD = BC. Then according to the definition of the parallelogram law, it is stated as

2(AB)² + 2 (BC)² = (AC)² + (BD)² . 

In case the parallelogram is a rectangle, then the law is stated as:

2(AB)² + 2(BC)² = 2(AC)²

Because in rectangle, two diagonals are of equal lengths. i.e., (AC = BD)

Let and  two vectors are acting simultaneously at a point 'O' . and  vectors are represented by  and  

OABD parallel is completed by drawing the line DB and AB. The diagonal OB denotes the value and direction of and 

We draw the perpendicular BE from B on the side OA produced.

 = 
 =  = 
 = 

Now, 

a = || = OA 

b = || =OD=AB

c=||=OB

Angle between  and  is  ∠AOD = α and angle between  and  is ∠AOB =  θ

We know from triangle OBE , 

 ` (OB)^2 = (OE)^2 + (BE)^2 = (OA + AE)^2 + (BE)^2`

`= (OA)^2 + 2. OA . AE + (AE)^2 +(BE)^2`  

 `= (OA)^2 + ((AE)^2 + (BE)^2) + 2 . OA .AB . (AE)/(AB) `

 `= (OA)^2 + (AB)^2 + 2 .OA .AB . Cos α`

 `C^2 = a^2 + b^2 + 2ab cosα` 

 `C = \sqrt{a^2+b^2 + 2 ab cos α} `

`\tan\theta=(BE)/(OE) = ((AB . BE)/(AB))/(OA+AE)` `= ((AB).((BE)/(AB)))/(OA+(AB).((AE)/(AB))` 

`=(AB \sin\alpha)/(OA+AB\cos\alpha)`

`\tan\theta=(b\sin\alpha)/(a+b\cos\alpha)`

  🌑 Vector Algebra :

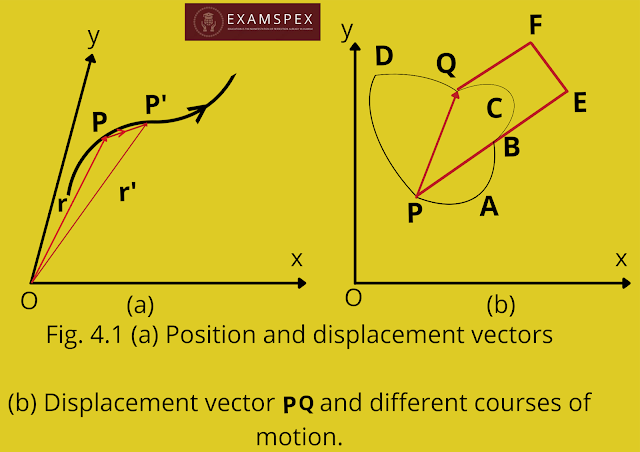
     ● Position and Displacement vector:

To describe the position of an object moving in a plane , we need to choose a convenient point . Say O as origin . Let P and P' be the positions of the object at time t and t' , respectively  (fig 4.1a) . We join O and P by a straight line. Then ,  is the position vector of the object at time t. An arrow is marked at the head of this line. It is represented by a symbol , i.e.  =.

Point P' is represented by another position vector,  denoted by 
. The length of the vector  represents the magnitude of the vector and it's direction is the direction in which P lies as seen from O. If the object moves from P to P' , the vector  is called the displacement vector corresponding to the motion from point P (at time t) to point P' (at time t').

It is important to note that displacement vector is the straight line joining the initial and final position and does not depend on the actual path undertaken by the object between the two positions. For example , in fig 4.1b , given the initial and final positions as P and Q, the displacement vector is the same   for different paths of journey , say PABCQ , PDQ and PBEFQ.

Therefore, the magnitude of displacement is either less or equal to the path length of an object between two points.

     ● Resolutions of vectors in two components :

 ■ Resolving Vectors along X and Y Axis-

To resolve a vector on an X-Y plane, first, draw the vector. Then, label and create the constructions on the figure as mentioned below :

The complete figure seems to be like a parallelogram, further applying the Parallelogram law of vector addition. Herein, the two vectors  and  appears to be added by the parallelogram law of vector addition to obtain . Therefore, with this, we can say that  and  are the resolved output of  as  has been again broken back to its components. Here, is the x-component; and the y-component.

In order to find the magnitudes of each component, in △OBC:

`cos θ = (OB)/(OC)`

Therefore, OB = OC cos θ

Hence, ||  =| | cos θ [ Magnitude of x – component ]

`sin θ = (BC)/(OC)`

So, BC = OC sin θ;

Also, BC = OD ( Opposite sides of Rectangle );

Therefore,

||  = || sin θ [ Magnitude of y – component ]

   ● Product of two vectors :

■ DOT PRODUCT : 

The dot or scalar product of two vectors  and , denoted by .  , is defined as the product of the magnitudes of  and  and the cosine of the angle  between them. In symbols,

 .  = | || | cosθ, (0≤ θ≤π)

We emphasize that .  is a scalar and not a vector . 

Suppose  ,  and  are vectors and m is a scalar. Then the following laws hold :

▪︎.  =  .  Commutative Law for Dot Products 

▪︎ .(  +  ) = .  + .   Distributive Law

▪︎ m(. ) = (m).  = . (m) = (. )m

▪︎ \[\widehat{i}.\widehat{i} = \widehat{j}.\widehat{j} = \widehat{k}.\widehat{k}=1\] \[\widehat{i}.\widehat{j}=\widehat{j}.\widehat{k}=\widehat{k}.\widehat{i}=0\]

▪︎ If .  = 0 and  and  are not null vectors, then  and  are perpendicular . 

There is a simple formula for .  when the unit vectors `\hat{i}, \hat{j}, \hat{k}` are used.

Given  =`A_1\hat{i} + A_2\hat{j} + A_3\hat{k}` and  = `B_1\hat{i} + B_2\hat{j} + B_3\hat{k}` . Then

.  = `A_1B_1 + A_2B_2 + A_3B_3`

Suppose  = `A_1\hat{i} + A_2\hat{j} + A_3\hat{k}` . Then.   = `A_1^2+A_2^2+A_3^2` .

■ CROSS PRODUCT : 

The cross product of vectors  and  is a vector   =  ×  defined as follows. The magnitude of  =  ×  is equal to the product of the magnitudes of  and  and the sine of the angle θ between them. The direction of  =  ×  is perpendicular to the plane of  and  so that  ,  and  form a right-handed system. In symbols,  ×  = ||| | sinθ  , (0 ≤ θ ≤ π)

Where   is a  unit vector indicating the direction of   ×  . ( Thus =  ,  and   form a right handed system)

If  =  , or if   is parallel to  , then sinθ = 0 and we define  ×  = 0.

Suppose  ,  and  are vectors and m is a scalar. Then the following laws hold:

▪︎  ×  = - (×) Commutative Law for Cross Products Fails

▪︎  ×(  + ) =  ×  +  x  Distributive Law

▪︎ m( × ) = (m )×  =  ×(m  )= ( × )m

▪︎ `\hat{i}x\hat{i}=\hat{j}x\hat{j}=\hat{k} x \hat{k}=0, \hat{i} x \hat{j}=\hat{k}, \hat{j} x \hat{k}=\hat{i}, \hat{k} x \hat{i}=\hat{j}`

▪︎ If  ×  = 0 and  and  are not null vectors, then  and  are parallel. 

▪︎ The magnitude of  ×  is the same as the area of a parallelogram with sides  and .

There is a simple formula   ×  when the unit vectors `\hat{i}, \hat{j}, \hat{k}` are used. 

Given, = `A_1i+ A_2j +A_3k` and  = `B_1i+ B_2j +B_3k` then,

 ×  = `|[i, j ,k], [A_1, A_2, A_3], [B_1, B_2, B_3]|` = `|[A_2 A_3], [B_2 B_3]|\hat{i} - |[A_1 A_3],[B_1 B_3]|\hat{j}+|[A_1 A_2],[B_1 B_2]|\hat{k}`  

■ TRIPLE PRODUCTS: 

Dot and cross multiplication of three vectors  ,  and  may produce meaningful products , called triple products, of the form ( .  ) ,  .(  ×  ) and ×(  ×  ) .

Suppose  ,  and  are vectors and m is a scalar. Then the following laws hold:

▪︎ In general, ( .  )  ≠  (  . ).

▪︎  .(  ×  ) =   .(  ×  ) =  . ( ×  ) = volume of a parallelepipedaving  ,  and  as edges, or the negative of this volume, according as  ,  and  do or do not form a right-handed system.

▪︎ In general,×(  ×  ) ≠( ×  )×  (Associative Law for Cross Products Fails)

▪︎ ×(  ×  ) =( .  )  - ( . )  

  ( ×  )×  =( .  )  - ( .  ) 

There is a simple formula for  .(  ×  ) when the unit vectors `\hat{i}, \hat{j}, \hat{k}` are used.

Given  =`A_1\hat{i} + A_2\hat{j} + A_3\hat{k}` ,  = `B_1\hat{i} + B_2\hat{j} + B_3\hat{k}` ,   = `C_1\hat{i} + C_2\hat{j} + C_3\hat{k}` . Then

 .(  ×  ) = `|[A_1\ A_2 \ A_3], [B_1\ B_2 \ B_3], [C_1\ C_2 \ C_3]|`